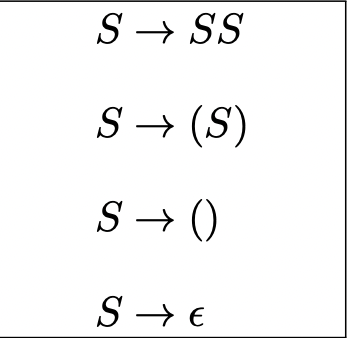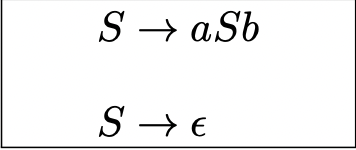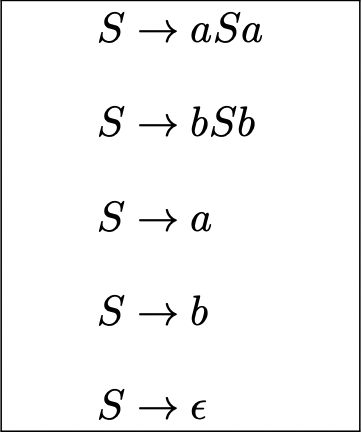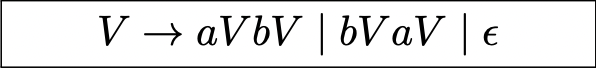编译原理06-parser-cfg

六、上下文无关文法-CFG

Definition-(Context-Free Grammar(CFG), 上下文无关文法)

上下文无关文法$G$是一个四元组$G = (T,N,S,P)$

1. $T$是终结符号（Terminal）集合，对应于词法分析器产生的词法单元

2. $N$是非终止符号（Non-terminal）集合

3. $S$是开始（start）符号$(S \in N)$且唯一

4. $P$是产生式（Production）集合

   $A \in N \to \alpha \in (T \cup N)^*$

   头部/左部（Head）A：单个非终结符

   体部/右部（Body）$\alpha$：终结符与非终结符构成的串，也可以是空串$\epsilon$

[Entended] Backus-Naur form ([E]BNF)

CFG

语义

语义：上下文无关文法$G$定义了一个语言$L(G)$

语言是串的集合

推导

$E \to E + E \mid E * E \mid (E) \mid -E \mid id$

推导即是将某个产生式的左边替换成它的右边

每一步推导需要选择替换哪个非终结符号，以及使用哪个产生式

$E \Rightarrow -E \Rightarrow -(-E) \Rightarrow \\ -(E+E) \Rightarrow -(id + E) \Rightarrow -(id+id) \\ E \Rightarrow -E :经过一步推导得出 \\ E \stackrel{\mathrm{+}}{\Rightarrow} -(id+E):经过一步或者多步推导得出 \\ E \stackrel{\mathrm{*}}{\Rightarrow} -(id+E)：经过零步或者多步得出$

定义

Definition(Sentential Form-句型)

$如果 S \stackrel{\mathrm{*}}{\Rightarrow} \alpha ,且 \alpha \in (T \cup U)^*\\ ,则称\alpha是文法G的一个句型$

Definition(Sentence-句子)

$如果S\stackrel{\mathrm{*}}{\Rightarrow} w,且w \in T^* \\ 则称w是文法G的一个句子$

Definition(文法$G$生成的语言$L( G)$)

文法$G$生成的语言$L( G)$是它能够推导出的所有句子的构成的集合

$w \in L(G) \Leftrightarrow S \stackrel{\mathrm{*}}{\Rightarrow} w$

文法G的两个基本问题

Membership问题：给定字符串$x \in T^*,x \in L(G)$?

即检查$x$是否符合文法$G$

这就是语法分析器的任务：

为输入的词法单元流寻找推导，构建语法分析树，或者报错

$L(G)$究竟是什么

这是程序设计语言设计者需要考虑的问题

Example

$L(G) = \lbrace 良匹配括号串 \rbrace$

$L(G) = \lbrace a^n b^n \mid n \geqslant 0 \rbrace$

$字母表\Sigma = \lbrace a, b\rbrace上的所有回文串构成的语言$

$\lbrace x \in \lbrace a, b \rbrace^* \mid x中a,b个数相同\rbrace$

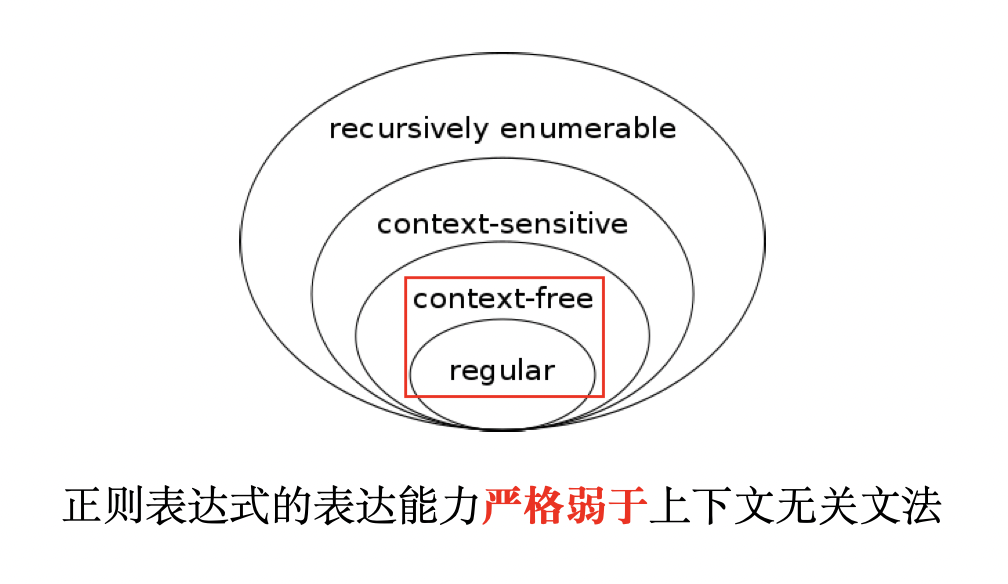
为什么不使用优雅，强大的正则表达式描述程序设计语言的语法

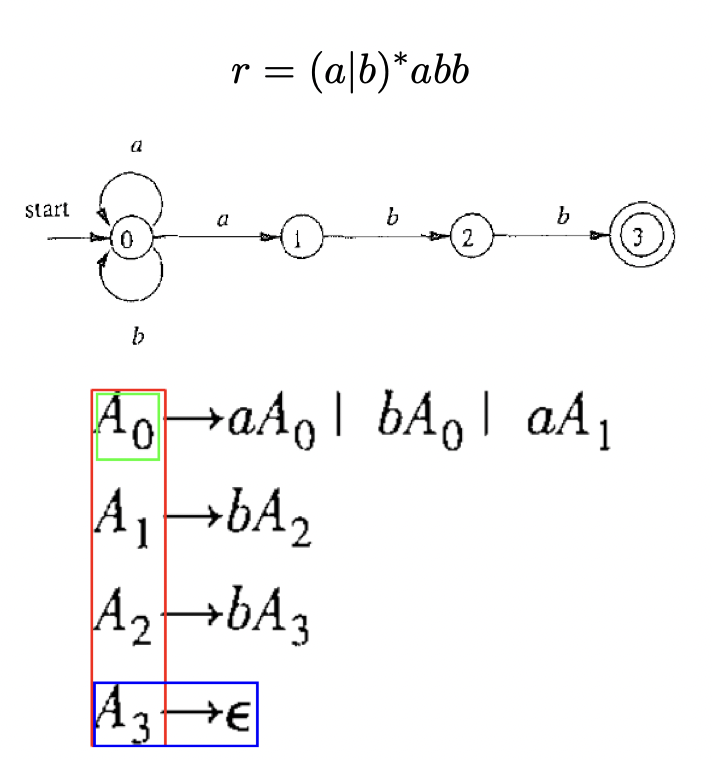
每个正则表达式$r$对应的语言$L(r)$都可以使用上下文无关文法来描述

此外，若$\delta(A_i,\epsilon)=A_j$，则添加$A_i \to A_j$

Theorem

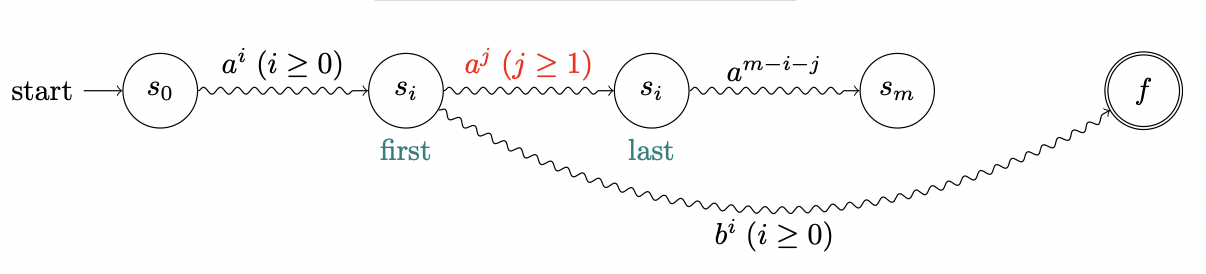
$L = \lbrace a^n,b^n \mid n \geqslant 0\rbrace$该语言无法使用正则表达式来描述

$反证法\\ 假设存在正则表达式r:L(r) = L \\ 则存在有限状态自动机D(r): L(D(r)) = L;设状态数为k \\ 考虑输入a^m , m \gt k \\$

$D(r)也能接受a^{i+j}b^i \Rightarrow 矛盾！$