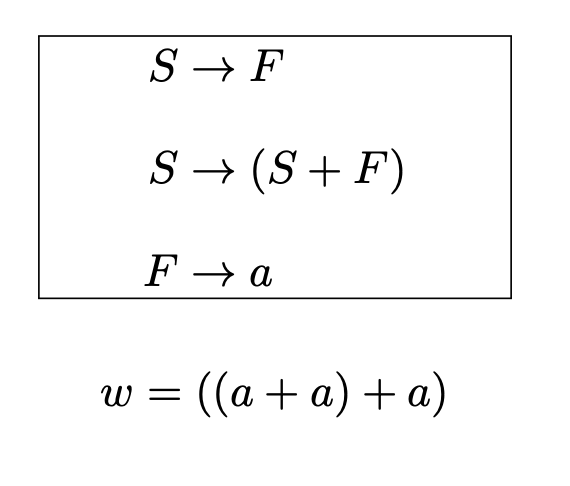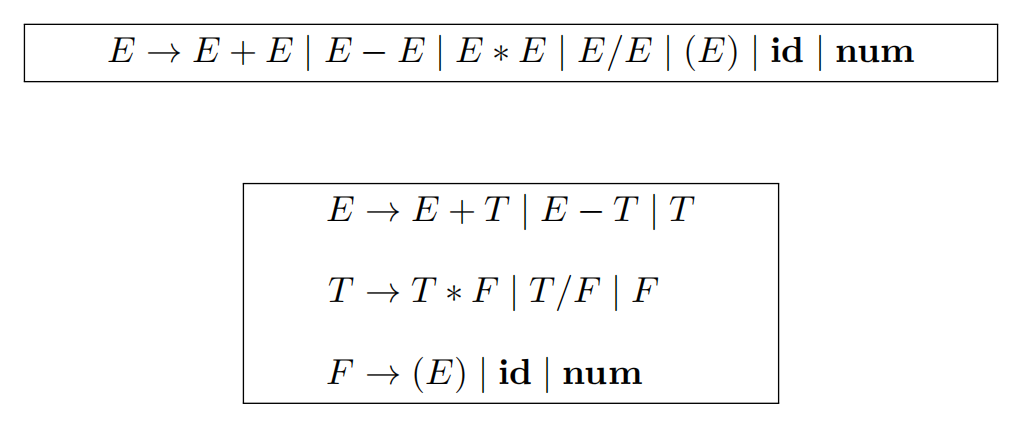编译原理07-parser-II

七、递归下降的LL(1)语法分析器

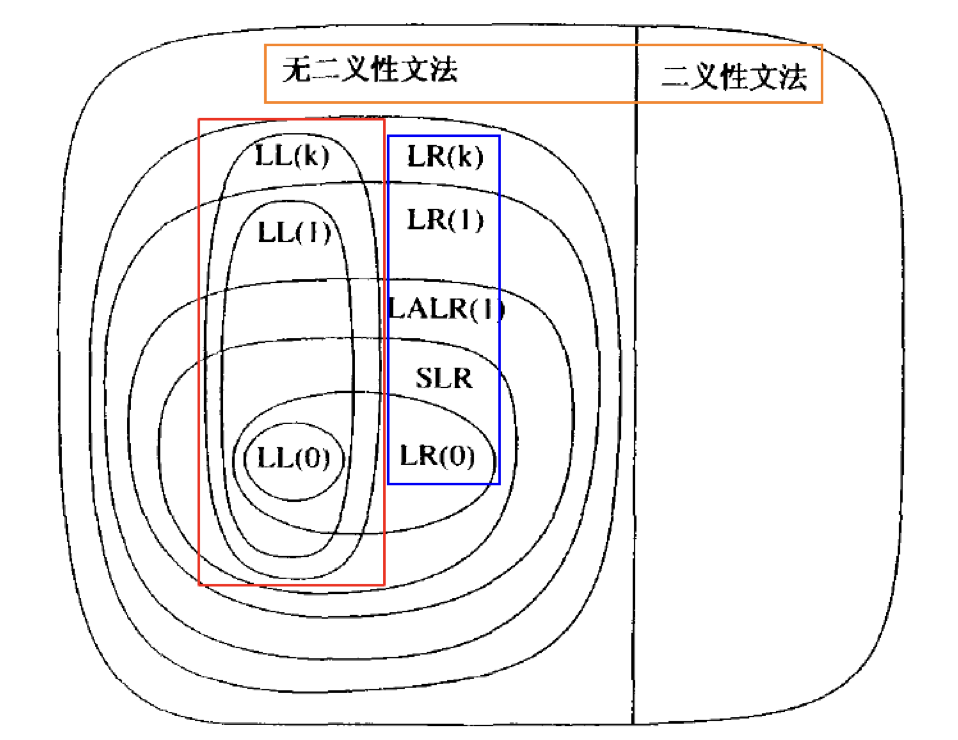
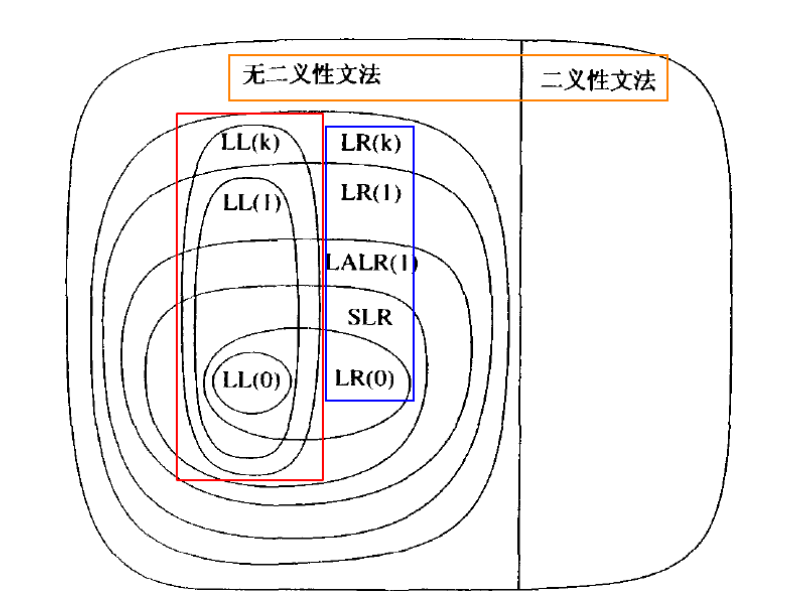
构建语法分析树：自顶向下 $vs.$ 自底向上

只考虑无二义性的文法
这意味着, 每个句子对应唯一的一棵语法分析树

LL(1)语法分析器的特点

自顶向下的

自顶向下构建语法分析树

1. 根结点是文法的起始符号$S$

2. 每个中间节点表示对某个非终结符应用某个产生式进行推导

   $Q: 选择哪个非终结符，以及选择哪个产生式$

3. 叶节点是词法单元流$w$ $

   仅包含终结符与特殊的文件结束符$$(EOF)$

4. 每个中间节点表示对某个非终结符应用某个产生式进行推导

   $Q：选择哪个非终结符，以及选择哪个产生式$

5. 在推导的每一步，$LL(1)$总是选择最左边的非终结符进行展开

   $LL(1)：从左向右读入词法单元$

递归下降的

递归下降的典型实现框架

为每一个非终结符写一个递归函数

内部按需调用其它的非终结符对应的递归函数，下降一层

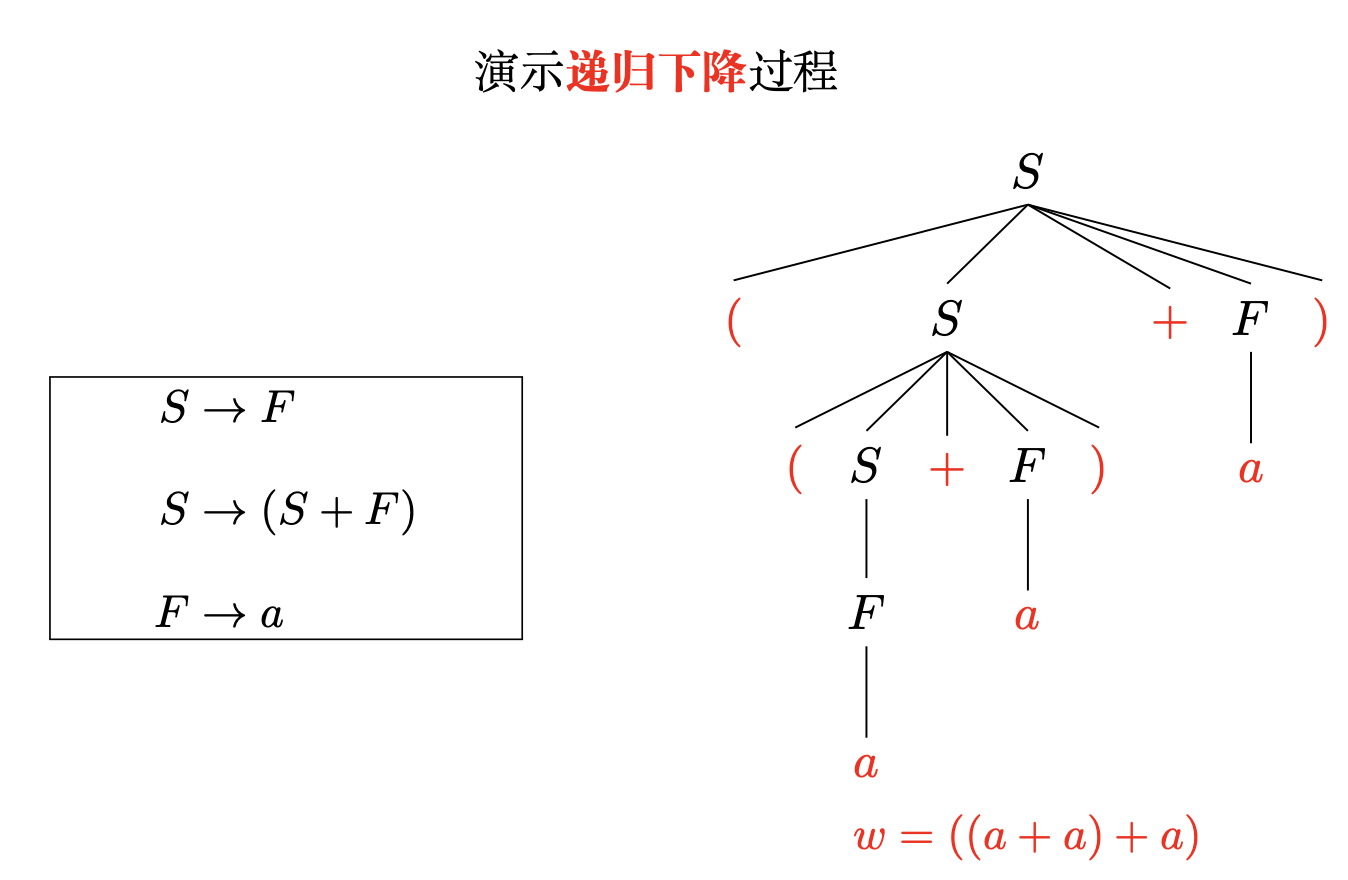
过程演示

每次都选择语法分析树最左边的非终结符进行展开

思考

同样是展开非终结符 S, 为什么前两次选择了 S → (S + F), 而第三次选择了 S → F?

因为它们面对的当前词法单元不同

第一次与第二次展开时，只有第二条会产生小括号

第三次展开时，期望匹配的为a，而第二条会产生小括号，所以选择第一条展开

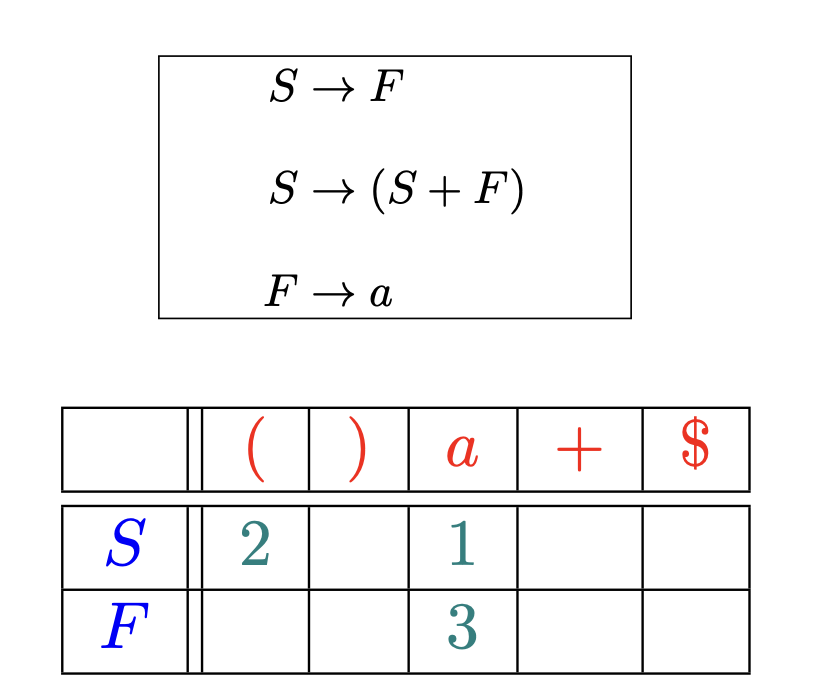
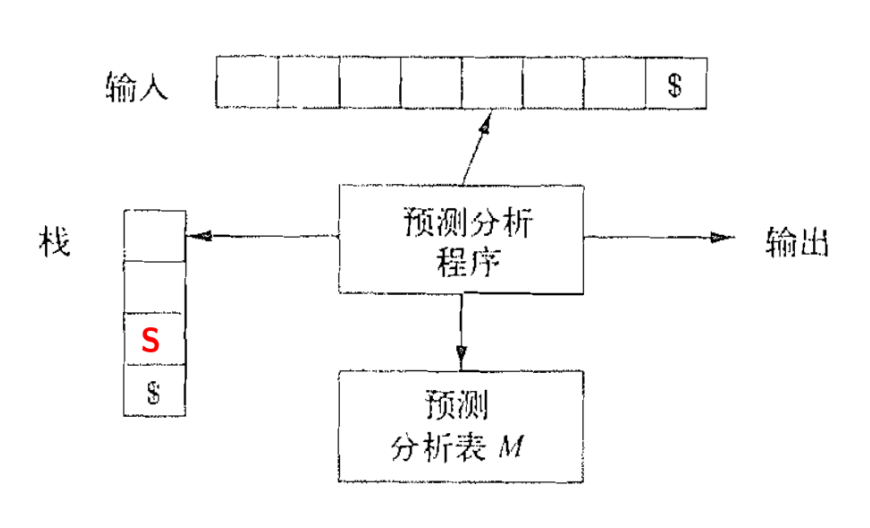
基于预测分析表的

使用预测分析表确定表达式

指明了每个非终结符在面对不同的词法单元或文件结束符时

该选择哪个产生式 (按编号进行索引) 或者报错 (空单元格)

适用于LL(1)文法的

Definition(LL(1)文法)

$$如果文法G的预测分析表是无冲突的，则G是LL(1)文法 \\ 无冲突：每个单元格里只有一个产生式(编号)$$

对于当前选择的非终结符，仅根据输入中的当前词法单元$LL(1)$即可确定需要使用哪条产生式

示例

再看递归下降中的例子

预测分析表的构建

先看一个例子

基础概念

Definition($FIRST(\alpha)$集合)

$FIRST(\alpha)$是可从$\alpha$推导得到的句型的首终结符号的集合

$$对于任意的（产生式的右部）\alpha \in (N \cup T)^* :\\ FIRST(\alpha) = \lbrace t \in T \cup \lbrace \epsilon \rbrace \mid \alpha \stackrel{\mathrm{*}}{\Rightarrow} t \beta \,\, \vee \,\, \alpha \stackrel{\mathrm{*}}{\Rightarrow} \epsilon \rbrace$$

考虑非终结符A的所有产生式$A \to \alpha_1, \, A \to \alpha_2,\, … ,\, A \to \alpha_3$，如果它们对应的$FIRST(\alpha_i)$集合互不相交，则只需要查看当前输入的词法单元，即可确定选择哪个产生式（或者报错）

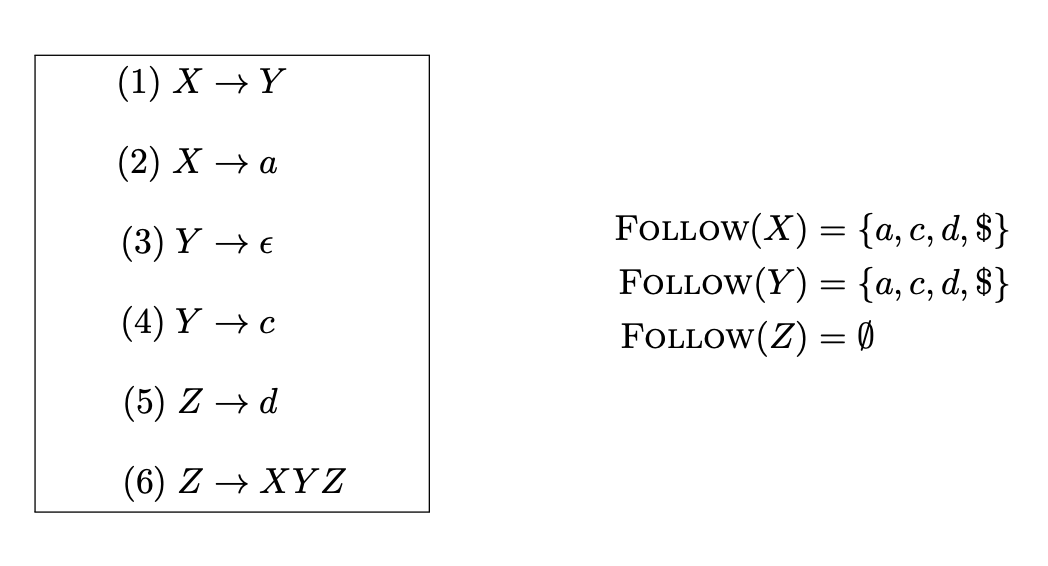
Definition($FOLLOW(\alpha)$集合)

$FOLLOW(\alpha)$是可能在某些句型中紧跟在 A 右边的终结符的集合

$$对于任意的 (产生式的左部) 非终结符 A \in N : \\ FOLLOW(A) = \lbrace t \in T \cup \lbrace \$ \rbrace \mid \exist s.S \stackrel{\mathrm{*}}{\Rightarrow} s \stackrel{\mathrm{\Delta}}{=} \beta A t \gamma \rbrace$$

考虑产生式$A \to \alpha$，如果从$\alpha$可能推导出空串($\alpha \stackrel{\mathrm{*}}{\Rightarrow} \epsilon$)，则只有当当前词法单元$t \in FOLLOW(A) $，才可以选择该产生式

如何计算给定文法G的预测分析表

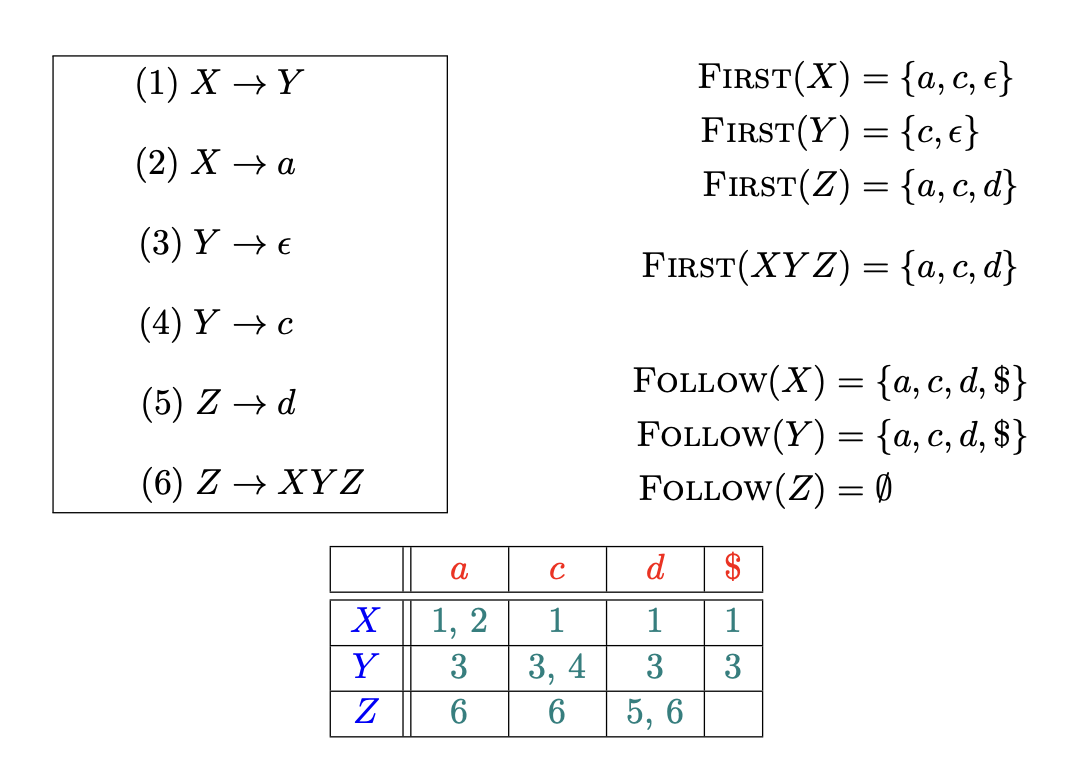
先计算每个符号 $X$ 的 $First(X)$ 集合

再计算每个符号串 $\alpha$ 的 $First(\alpha)$ 集合

例

为每个非终结符 $X$ 计算 $Follow(X)$ 集合

例

根据$First$与$Follow$集合计算给定文法G的预测分析表

$$对应每条产生式 A \to \alpha 与终结符 t，如果 \\\\ t \in FIRST(\alpha) \\\\ \alpha \stackrel{\mathrm{*}}{\Rightarrow} \epsilon \,\wedge\, t \in FOLLOW(A) \\\\ 则在表格[A,t]中填入 A \to \alpha （编号）$$

Definition（$LL(1)$文法）

$$如果文法 G 的预测分析表是无冲突的, 则 G 是 LL(1) 文法。$$

结论

$$t \in FIRST(\alpha) \\ \epsilon \in FIRST(\alpha) \, \wedge \, FOLLOW(A) \\ 当下的选择未必正确, 但'你别无选择'。$$

LL(1)语法分析器

$$L: 从左向右(left-to-right)扫描输入\\ L: 构建最左(leftmost)推导\\ 1: 只需向前看一个输入符号便可确定使用哪条生成式$$

What is LL(0)?

非递归的预测分析算法

非LL(1)文法的处理方法

改造它

1. 消除左递归
2. 提取左公因式

Example

$$FIRST(E + T) \cap FIRST(T) \neq \Phi \rightarrow 不是LL(1)文法$$

E在不消耗任何词法单元的情况下，直接递归调用E，造成死循环

改写成“右递归”文法

文件结束符$的用处

直接左递归(Direct Left Recursion)

拓展为

间接左递归(Indirect Left Recursion)

算法要求

1. 文法中不存在环（形如$A \stackrel{\mathrm{*}}{\Rightarrow} A$的推导）
2. 文法中不存在$\epsilon$产生式（形如$A \rightarrow \epsilon$的产生式）

$$S \rightarrow A\, a \mid b \\ A \rightarrow A \, c \mid S \, b \mid \epsilon$$

提取左公因式(Left-Factoring)

很显然，提取左公因式无助于消除文法二异性