树（Tree）

二叉树 - binary tree

二叉树是一种非线性数据结构，代表“祖先”与“后代”之间的派生关系，体现了“一分为二”的分治逻辑。与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用。

在java中可以这么定义一个TreeNode

1
2
3
4
5
6
7
/* 二叉树节点类 */
class TreeNode {
    int val;         // 节点值
    TreeNode left;   // 左子节点引用
    TreeNode right;  // 右子节点引用
    TreeNode(int x) { val = x; }
}

每个节点都有两个引用（指针），分别指向「左子节点 left-child node」和「右子节点 right-child node」，该节点被称为这两个子节点的「父节点 parent node」。当给定一个二叉树的节点时，我们将该节点的左子节点及其以下节点形成的树称为该节点的「左子树 left subtree」，同理可得「右子树 right subtree」。

二叉树术语

这里列举一点容易忘记的

  • 节点所在的「层 level」：从顶至底递增，根节点所在层为 1 （最好根据题目，笔者记得在学数据结构时有的题目根节点会记为0）。
  • 节点的「度 degree」：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
  • 二叉树的「高度 height」：从根节点到最远叶节点所经过的边的数量。
  • 节点的「深度 depth」：从根节点到该节点所经过的边的数量。
  • 节点的「高度 height」：从距离该节点最远的叶节点到该节点所经过的边的数量。

常见二叉树

  • 完美二叉树

    所有层的节点都被完全填满。在完美二叉树中，叶节点的度为0，其余所有节点的度都为2；若树的高度为h，则节点总数为 2h+1−1 ，呈现标准的指数级关系，反映了自然界中常见的细胞分裂现象。

  • 完全二叉树

    「完全二叉树 complete binary tree」只有最底层的节点未被填满，且最底层节点尽量靠左填充。

  • 完满二叉树

    完满二叉树 full binary tree」除了叶节点之外，其余所有节点都有两个子节点。

  • 平衡二叉树

    平衡二叉树 balanced binary tree」中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。

二叉树遍历

二叉树常见的遍历方式包括层序遍历、前序遍历、中序遍历和后序遍历等。这里以java实现。

层序遍历

「层序遍历 level-order traversal」从顶部到底部逐层遍历二叉树，并在每一层按照从左到右的顺序访问节点。

层序遍历本质上属于「广度优先遍历 breadth-first traversal」，也称「广度优先搜索 breadth-first search, BFS」，它体现了一种“一圈一圈向外扩展”的逐层遍历方式。

广度优先遍历通常借助“队列”来实现。队列遵循“先进先出”的规则，而广度优先遍历则遵循“逐层推进”的规则，两者背后的思想是一致的。实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* 层序遍历 */
List<Integer> levelOrder(TreeNode root) {
    // 初始化队列，加入根节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    // 初始化一个列表，用于保存遍历序列
    List<Integer> list = new ArrayList<>();
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // 队列出队
        list.add(node.val);           // 保存节点值
        if (node.left != null)
            queue.offer(node.left);   // 左子节点入队
        if (node.right != null)
            queue.offer(node.right);  // 右子节点入队
    }
    return list;
}

前序、中序、后序遍历

前序、中序和后序遍历都属于「深度优先遍历 depth-first traversal」，也称「深度优先搜索 depth-first search, DFS」，它体现了一种“先走到尽头，再回溯继续”的遍历方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/* 前序遍历 */
void preOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：根节点 -> 左子树 -> 右子树
    list.add(root.val);
    preOrder(root.left);
    preOrder(root.right);
}

/* 中序遍历 */
void inOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 根节点 -> 右子树
    inOrder(root.left);
    list.add(root.val);
    inOrder(root.right);
}

/* 后序遍历 */
void postOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 右子树 -> 根节点
    postOrder(root.left);
    postOrder(root.right);
    list.add(root.val);
}

二叉搜索树

二叉搜索树 binary search tree 满足以下条件。

  1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
  2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1 。

二叉搜索树的中序遍历序列是升序的

AVL 树

AVL 树既是二叉搜索树，也是平衡二叉树，同时满足这两类二叉树的所有性质，因此是一种「平衡二叉搜索树 balanced binary search tree」。

由于 AVL 树的相关操作需要获取节点高度，因此我们需要为节点类添加 height 变量

AVL 树旋转

AVL 树的特点在于“旋转”操作，它能够在不影响二叉树的中序遍历序列的前提下，使失衡节点重新恢复平衡。换句话说，旋转操作既能保持“二叉搜索树”的性质，也能使树重新变为“平衡二叉树”。

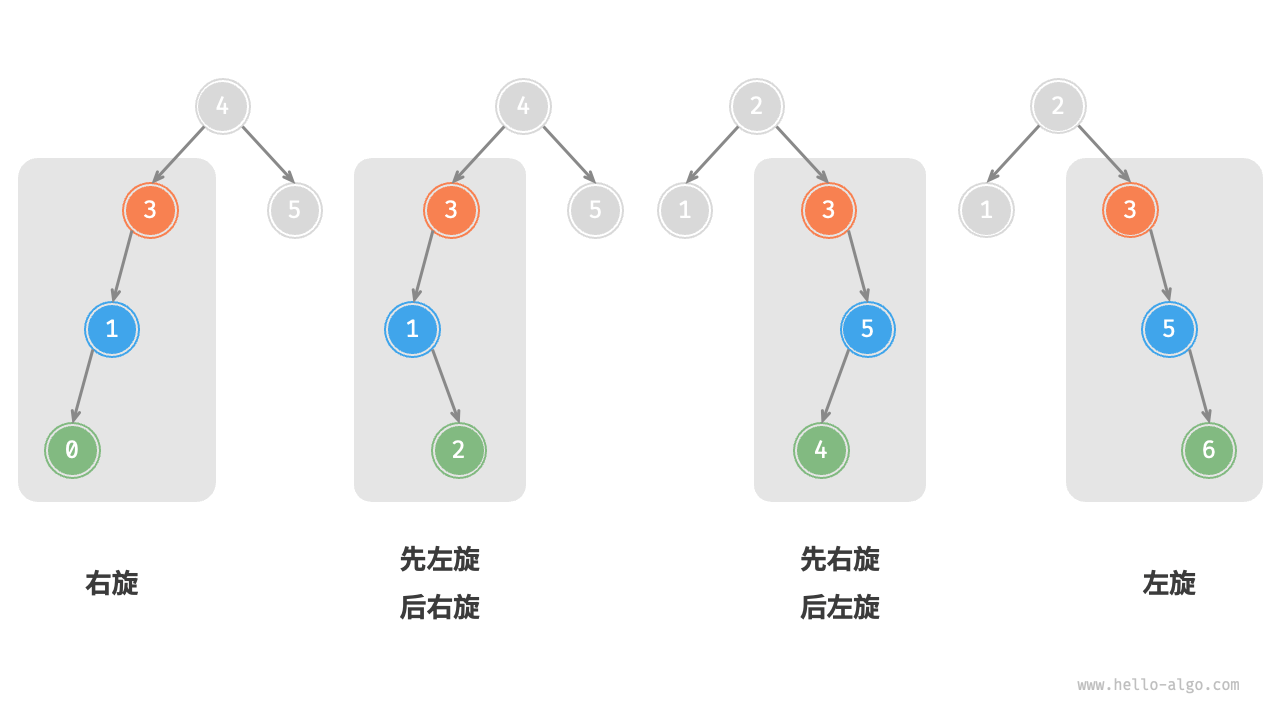
我们将平衡因子绝对值 >1 的节点称为“失衡节点”。根据节点失衡情况的不同，旋转操作分为四种：右旋、左旋、先右旋后左旋、先左旋后右旋。

  • 右旋

    我们关注以失衡节点为根节点的子树，将该节点记为 node ，其左子节点记为 child ，执行“右旋”操作。完成右旋后，子树恢复平衡，并且仍然保持二叉搜索树的性质。

    操作流程：

    1. 以 child 为原点，将 node 向右旋转

    2. 用 child 代替以前 node 的位置

    3. 当节点 child 有右子节点（记为 grand_child ）时，需要在右旋中添加一步：将 grand_child 作为 node 的左子节点。

  • 左旋

    相应地，如果考虑上述失衡二叉树的“镜像”，可以得到左旋的操作。我们关注以失衡节点为根节点的子树，将该节点记为 node ，其右子节点记为 child ，执行“左旋”操作。完成左旋后，子树恢复平衡，并且仍然保持二叉搜索树的性质。

    操作流程：

    1. 以 child 为原点，将 node 向左旋转
    2. 用 child 代替以前 node 的位置
    3. 当节点 child 有左子节点（记为 grand_child ）时，需要在左旋中添加一步：将 grand_child 作为 node 的右子节点。

  • 先左旋后右旋

    对于某些节点，仅使用左旋或右旋都无法使子树恢复平衡。此时需要先对 child 执行“左旋”，再对 node 执行“右旋”。

  • 先右旋后左旋

    对于某些节点，仅使用左旋或右旋都无法使子树恢复平衡。此时需要先对 child 执行“右旋”，再对 node 执行“左旋”。

旋转方式如何选择

这里借用了别人的图（侵权联系我删除）

我们也可以用表格来总结一下

失衡节点的平衡因子 子节点的平衡因子 旋转方法
> 1 & 左偏树 >= 0 右旋
> 1 & 左偏树 < 0 先左旋再右旋
< -1 & 右偏树 <= 0 左旋
< -1 & 右偏树 > 0 先右旋再左旋